Trabalho 1

Exemplo

http://www.openprocessing.org/sketch/3270

Modelo Natural

Tanto no exemplo como nos modelos foi utilizado a proporção áurea, também conhecida como a marca de Deus. Muitos elementos da natureza seguem esse estranho padrão, desde conchas à pessoas. Um exemplo é que se um humano “mediano” dividir sua altura pela distância entre o umbigo e a cabeça, o resultado será algo em torno de 1,618, que é o número áureo. (fonte: Mundo Estranho)

Além de estar presente na natureza, essa proporção também é muito usada no design. Com o objetivo de dar mais forma, simetria e equilíbrio ao produto, o designer emprega essa proporção para que o observador sinta empatia por ele.

Outros exemplos:

Modelo Matemático:

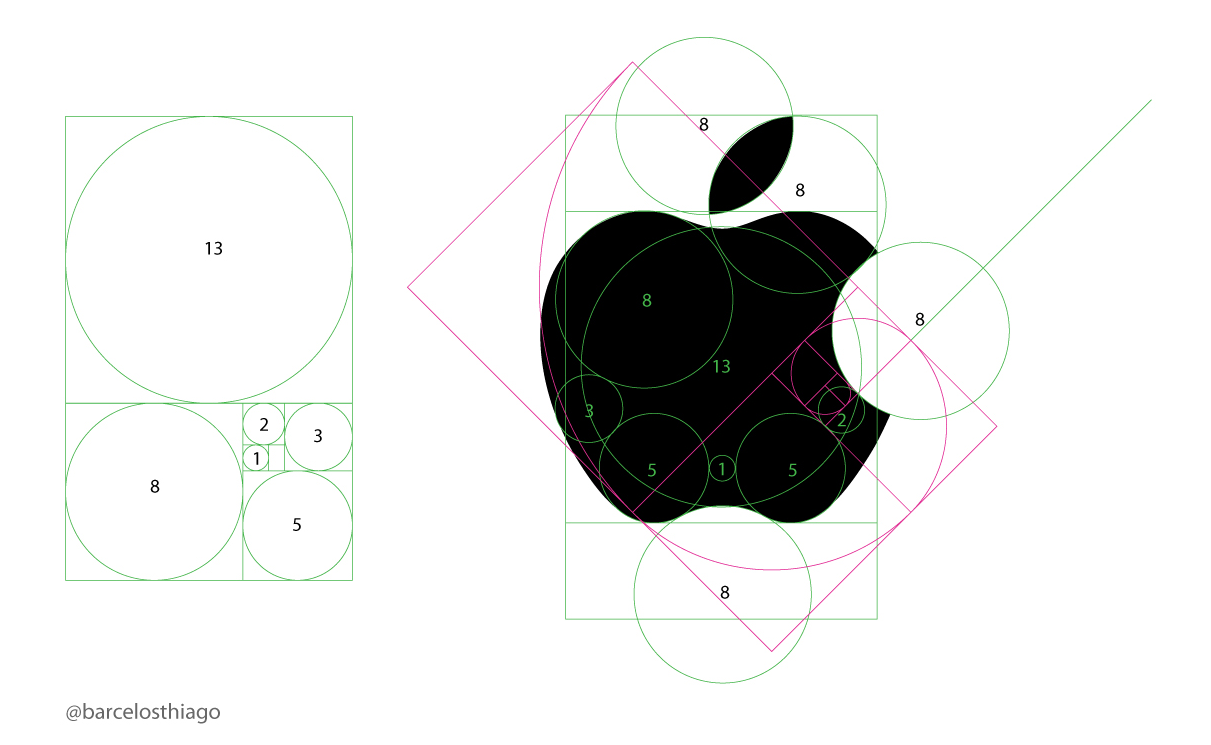
A proporção áurea é uma razão algébrica encontrada a partir da sequência de Fibonacci. Segundo essa sequência um número é obtido pela soma dos seus dois antecessores: 1, 1, 2, 3, 5, 8, 13... foi daí que se percebeu um padrão de 1,618 que vem sendo aplicado em vários segmentos, tanto na natureza de forma inexplicável, como na arte, arquitetura ou design.

Modelo computacional:

int maxDots = 700;
float g;
float gAng;
float rad;
float rgrowth;
float cur = 0;
float rot = 0;
float x,y;
float w = 2;
float h = 2;
float deg = 0.9992;
float colorInc;



void setup() {
size(800,800);
background(0); // cor do background
smooth(); // suaviza as formas
noFill(); // a elipse não será preenchida
colorMode(HSB);
strokeWeight(0.2); // espessura da borda
frameRate(80);

g = 1/1.618033989; //proporção áurea
gAng = 360-360 * g + 0; //ângulo da rotação
rad = 5; // distanciamento das formas
rgrowth = 1.004;
}

void draw() {
cur++; //Variável vai sempre somar mais um
rot += gAng;
rot -= int(rot/360) * 360; // rotação, distanciamento entre as elipses
rad *= rgrowth;
stroke(g*cur/3,g*cur/3,255); //Conforme a variável cur vai aumentando os valores da cor do stroke vão alterando.
x = cos(rot * PI/180) * rad + width/2; //posição X levando em conta o ângulo da rotação e a largura da tela
y = sin(rot * PI/180) * rad + height/2; //posição X levando em conta o ângulo da rotação e a altura da tela
ellipse(x,y,w,h);

w+=g/14; // largura do círculo
h+=g/14; // altura do círculo
}

 O exemplo do openprocessing é, basicamente, círculos transparentes com bordas coloridas girando na proporção áurea. O código se baseia na trigonometria para determinar os ângulos onde os círculos vão aparecer e, conforme isso vai acontecendo, as variáveis vão mudando para que as elipses apareçam conforme a proporção e para que as cores também mudem.