Pong com Padle

void barra(){
  rect(780, (mouseY - 30), 10, 60);
}
 
void moveBola() {
  fill(110,242,93);
  ellipse(dX,dY,20,20);
  t+=0.1;
  dX = vX*t;
  dY = vY*t;
  controleBola();
}
 
void controleBola(){
  if(dX < 10){
    dX = -dX;
  }else if(dX > 790){
    dX = -dX;
  }
}

A alteração necessária para o padle foi a adição de uma função que chama um rect cujo X é 780 e o Y leva em consideração a posição do mouse. O -30 foi adicionado com o intuito de que o mouse ficasse centralizado no padle de tamanho 60.

Yin-Yang

void setup() {
  size(600, 600);
  background(255);
  ellipse (300, 300, 300, 300); //elipse maior
  fill(1);
  arc(300, 300, 300, 300, 3*1.57, 2.5*3.14, PIE); //arco preto
  noStroke();
  fill(255);
  ellipse (300, 226, 150, 150);//elipse média preta
  fill(1);
  ellipse (300, 375, 150, 150); //elipse média branca
  ellipse (300, 225, 50, 50); //círculo menor de baixo
  fill(255);
  ellipse (300, 375, 50, 50); //circulo menor de baixo
 
 
}

O Yin-Yang consiste em uma elipse branca e um arco, ou o contrário. Depois são adicionadas mais duas elipses que vão até a metade da elipse maior em em seguida mais duas menores no centro das elipses médias.

Tarefa - Círculos crescendo

int i = 0;

int j = 0;

void setup(){

  size(600, 600);

  background(255);

  fill (0);

  circulos();

}

void circulos(){

     for (int y = 5; y < 650; y = y + 50) {

         j = j + 5;

         i = i + 5;

         for (int x = 10; x < 650; x = x + 50) {

           ellipse(x, y, i, j);

         }

     }

}

O código consiste em dois laços de repetição. No void setup, além das configurações comuns, é chamada a função "circulos()", que é onde se encontram as estruturas de repetição para a criação dos círculos. O primeiro vai determinar a  posição y e o tamanho das elipses; a cada repetição as elipses irão deslocar 50px no eixo y e aumentarão 5 no seu tamanho. O segundo laço irá alterar a posição da bola no eixo X em 50px sempre que for executado.

Trabalho 1

Exemplo

http://www.openprocessing.org/sketch/3270

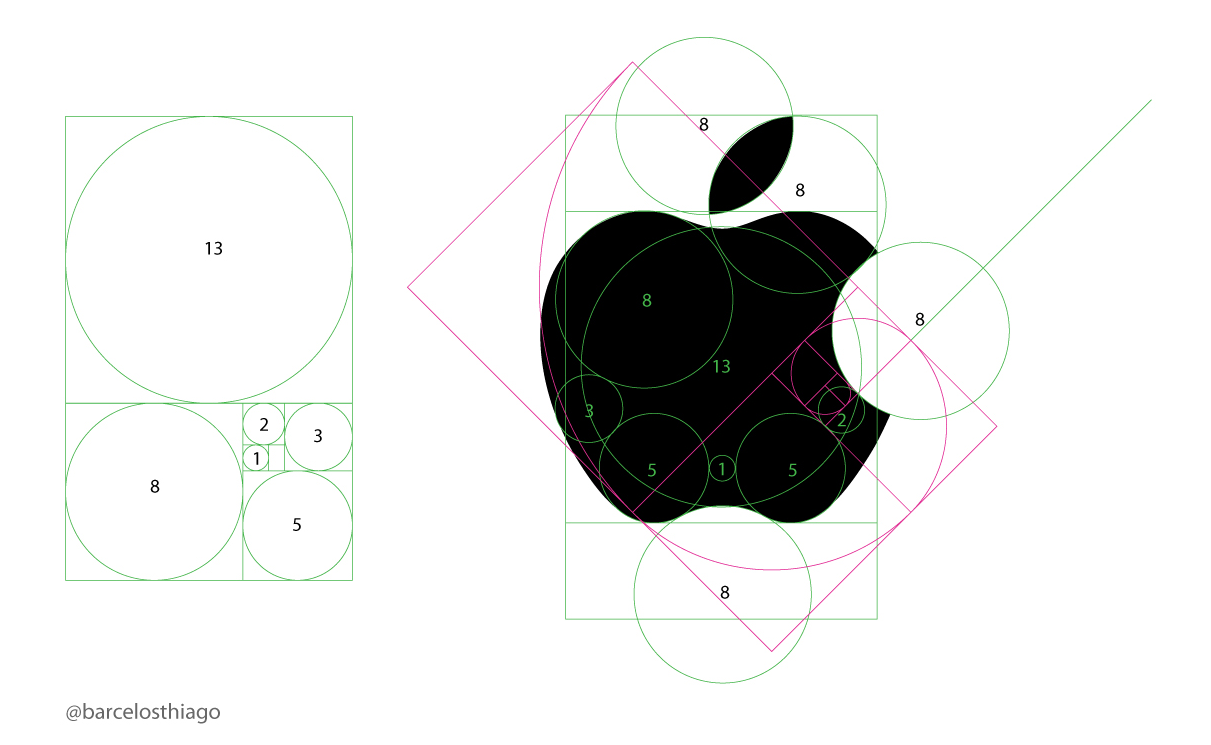
Modelo Natural

Tanto no exemplo como nos modelos foi utilizado a proporção áurea, também conhecida como a marca de Deus. Muitos elementos da natureza seguem esse estranho padrão, desde conchas à pessoas. Um exemplo é que se um humano “mediano” dividir sua altura pela distância entre o umbigo e a cabeça, o resultado será algo em torno de 1,618, que é o número áureo. (fonte: Mundo Estranho)

Além de estar presente na natureza, essa proporção também é muito usada no design. Com o objetivo de dar mais forma, simetria e equilíbrio ao produto, o designer emprega essa proporção para que o observador sinta empatia por ele.

Outros exemplos:

Modelo Matemático:

A proporção áurea é uma razão algébrica encontrada a partir da sequência de Fibonacci. Segundo essa sequência um número é obtido pela soma dos seus dois antecessores: 1, 1, 2, 3, 5, 8, 13... foi daí que se percebeu um padrão de 1,618 que vem sendo aplicado em vários segmentos, tanto na natureza de forma inexplicável, como na arte, arquitetura ou design.

Modelo computacional:

int maxDots = 700;
float g;
float gAng;
float rad;
float rgrowth;
float cur = 0;
float rot = 0;
float x,y;
float w = 2;
float h = 2;
float deg = 0.9992;
float colorInc;



void setup() {
size(800,800);
background(0); // cor do background
smooth(); // suaviza as formas
noFill(); // a elipse não será preenchida
colorMode(HSB);
strokeWeight(0.2); // espessura da borda
frameRate(80);

g = 1/1.618033989; //proporção áurea
gAng = 360-360 * g + 0; //ângulo da rotação
rad = 5; // distanciamento das formas
rgrowth = 1.004;
}

void draw() {
cur++; //Variável vai sempre somar mais um
rot += gAng;
rot -= int(rot/360) * 360; // rotação, distanciamento entre as elipses
rad *= rgrowth;
stroke(g*cur/3,g*cur/3,255); //Conforme a variável cur vai aumentando os valores da cor do stroke vão alterando.
x = cos(rot * PI/180) * rad + width/2; //posição X levando em conta o ângulo da rotação e a largura da tela
y = sin(rot * PI/180) * rad + height/2; //posição X levando em conta o ângulo da rotação e a altura da tela
ellipse(x,y,w,h);

w+=g/14; // largura do círculo
h+=g/14; // altura do círculo
}

 O exemplo do openprocessing é, basicamente, círculos transparentes com bordas coloridas girando na proporção áurea. O código se baseia na trigonometria para determinar os ângulos onde os círculos vão aparecer e, conforme isso vai acontecendo, as variáveis vão mudando para que as elipses apareçam conforme a proporção e para que as cores também mudem. 

Observação de um exemplo do Processing

Exemplo:

http://processing.org/examples/linear.html

Código:

float a;

void setup() {
  size(640, 360);
  stroke(255);
  a = height/2;
}

void draw() {
  background(51);
  line(0, a, width, a);  
  a = a - 0.5;
  if (a < 0) { 
    a = height; 
  }
}

Observação:

A variável "a" vai determinar a posição da linha. No setup ela está determinando onde ela vai aparecer, no caso na altura da tela sobre dois, ou seja, na metade da tela. No draw ela vai determinar a animação, pois, como está especificado na terceira linha do void draw, a cada atualização do background, a variável "a" irá subtrai, vai alterar a posição da linha em 0.5. Quando "a" for menor que 0, ou seja, sair da tela, ela receberá o valor de "height" fazendo com que a linha vá para a parte inferior da tela e a animação ocorra mais uma vez.